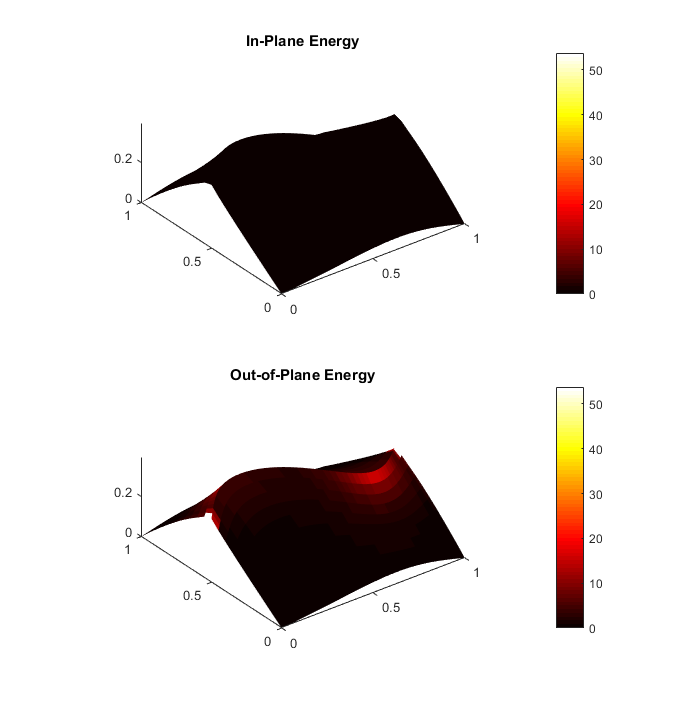
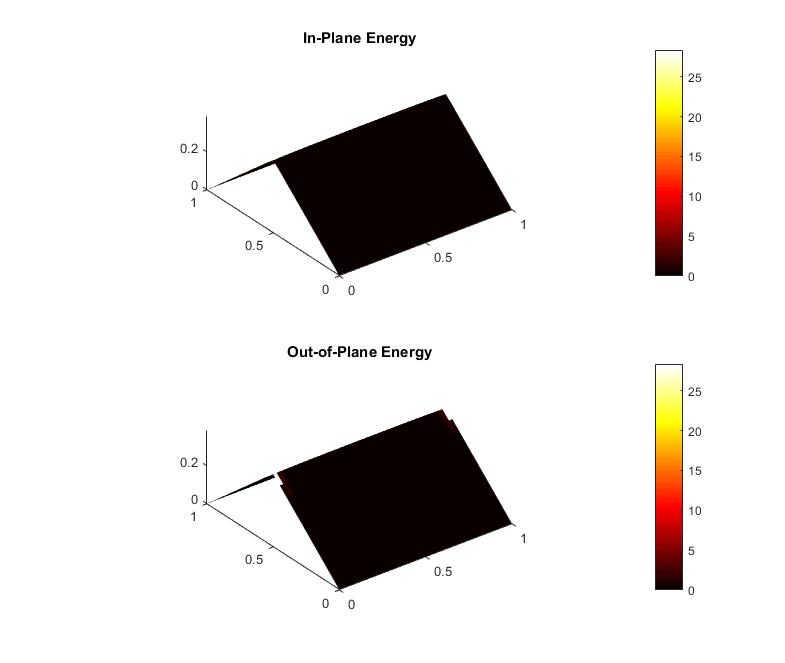
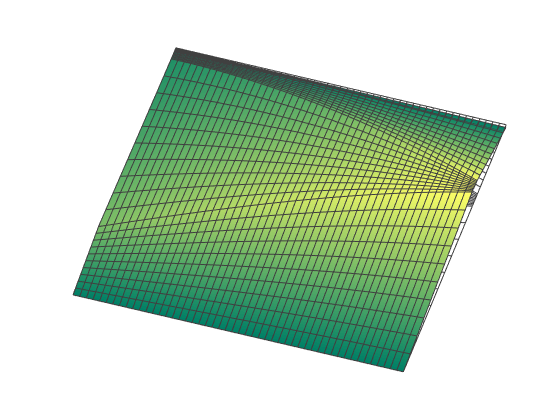
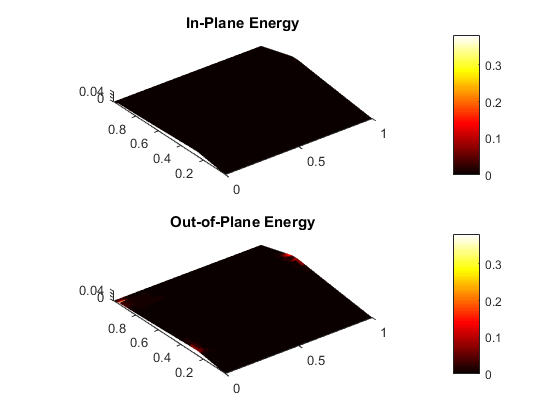
Finite element modeling of curved-crease origami
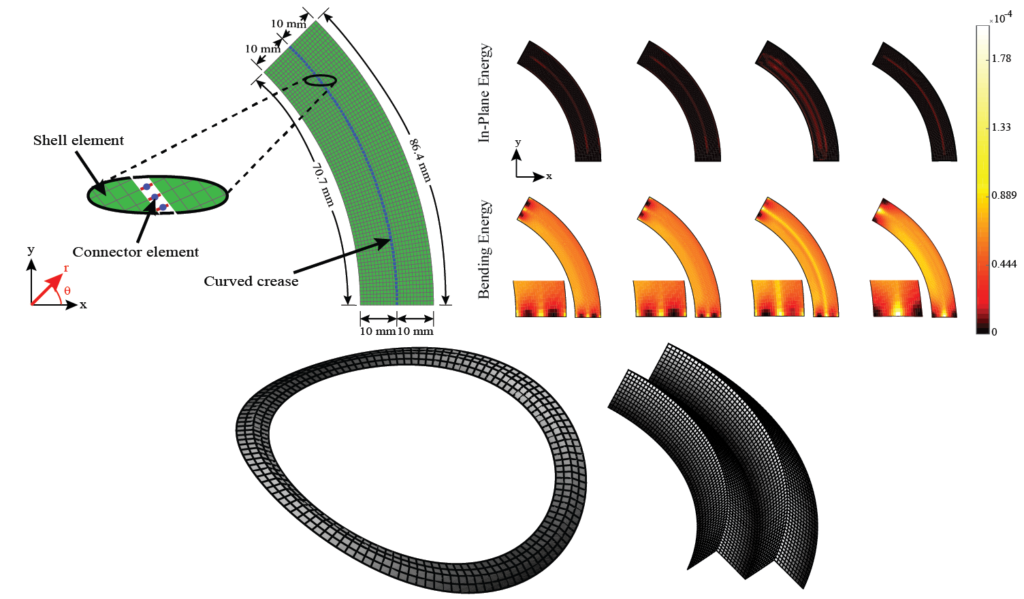
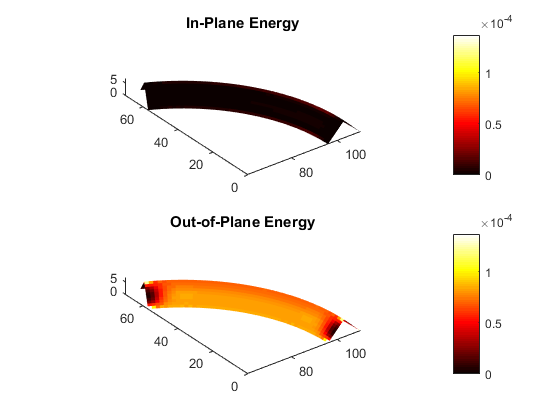
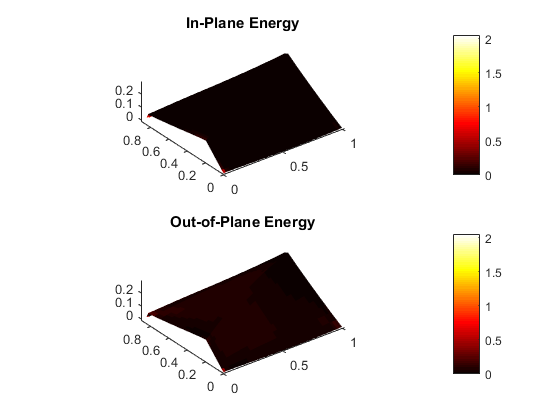
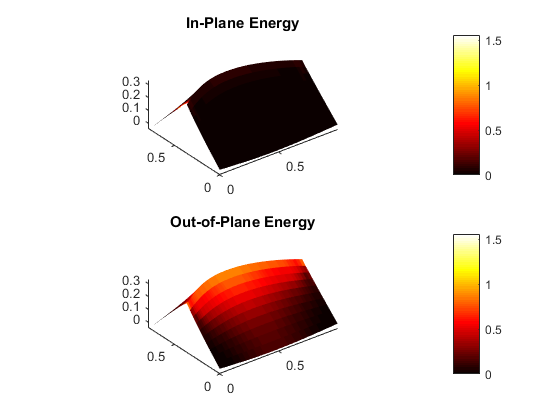
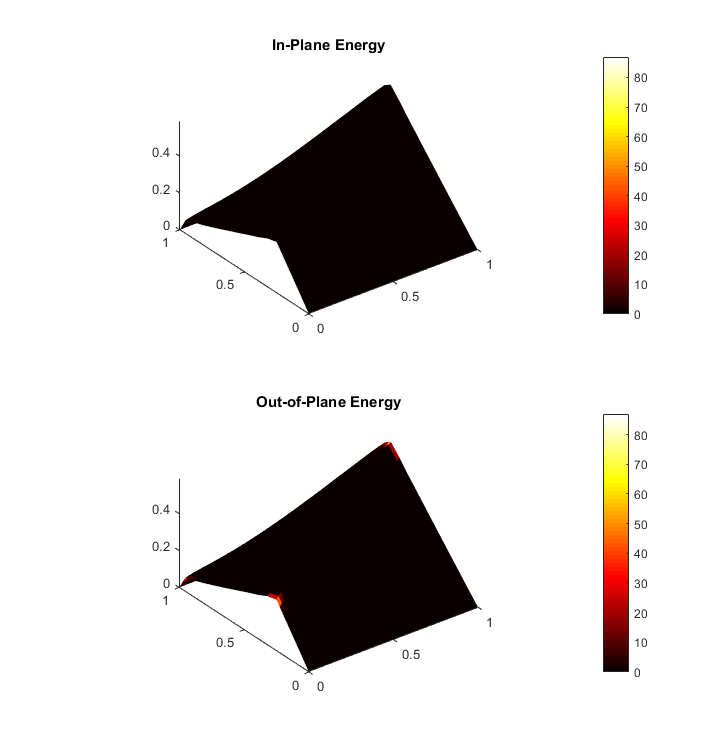
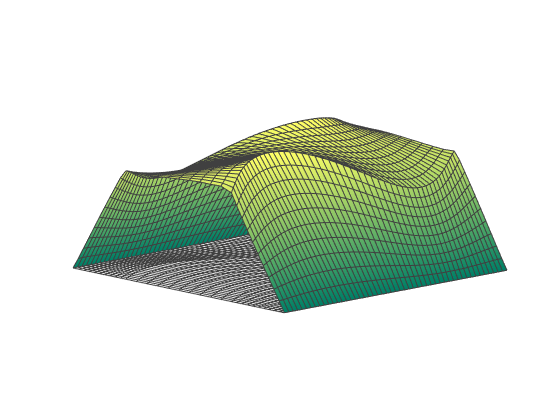
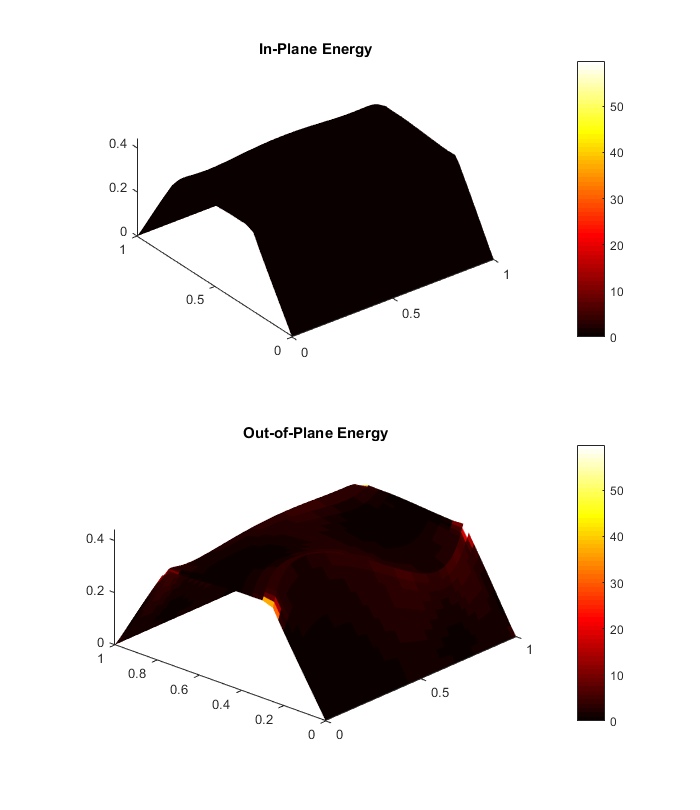
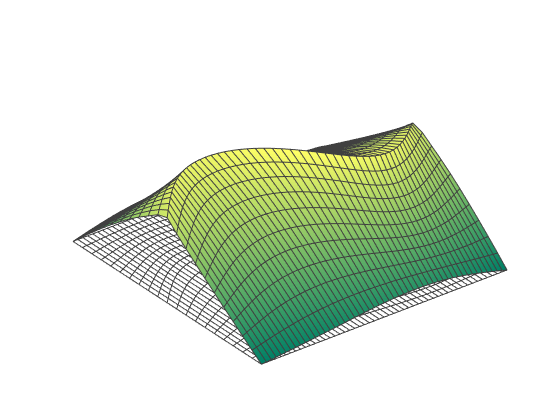
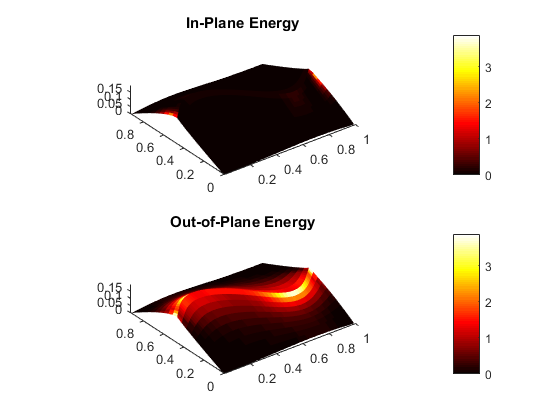
Finite element modeling is an essential tool for structural engineers. Although simple or highly idealized structures have analytical expressions describing their force-deformation response (for instance, slender beams and truss bars), most structures are too complicated to find a closed-form solution. Finite element analysis involves a computer solving thousands of linear equations formed by dividing structures into small parts which have simple deformation modes. For curved-crease origami analysis, finite elements offers much information about the stresses and strains in the curved sheets.
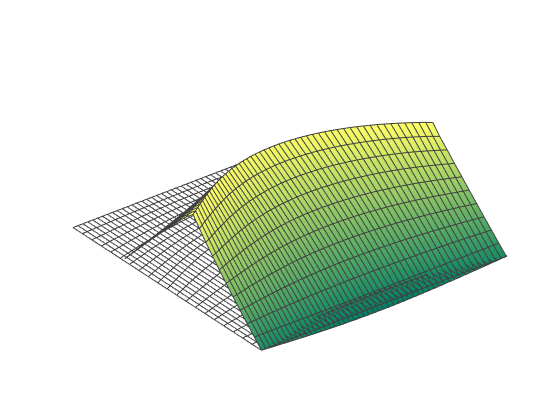
Finite elements can model the folding and post-folding structural response of curved-crease origami with large deformations. However, as models become more complex (more creases, higher curvatures), the finite element analysis process becomes incredibly slow with long computer run times. Also, as models become more complex, convergence issues arise which requires engineers to employ more complicated modeling techniques that further slow down the analysis. If the engineer is looking for an optimal fold pattern or is trying out different fold patterns to see what shapes form after folding, finite elements may be too complicated and unreliable.
One solution for these problems of speed and reliability is bar and hinge modeling.